题目

Cutting Towers

[1600]

There is a toy building consisting of n towers. Each tower consists of several cubes standing on each other. The i-th tower consists of hi cubes, so it has height hi.

Let’s define operation slice on some height H as following: for each tower i, if its height is greater than H, then remove some top cubes to make tower’s height equal to H. Cost of one “slice” equals to the total number of removed cubes from all towers.

Let’s name slice as good one if its cost is lower or equal to k (k≥n).

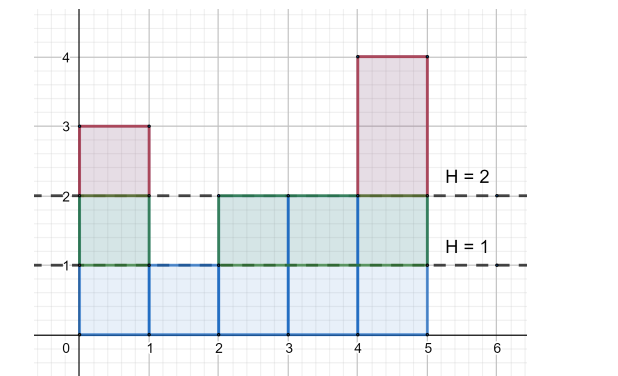
image

Calculate the minimum number of good slices you have to do to make all towers have the same height. Of course, it is always possible to make it so.

Input
The first line contains two integers n and k (1≤n≤2⋅105, n≤k≤109) — the number of towers and the restriction on slices, respectively.
The second line contains n space separated integers h1,h2,…,hn (1≤hi≤2⋅105) — the initial heights of towers.

Output
Print one integer — the minimum number of good slices you have to do to make all towers have the same heigth.

思路

整体策略

我们的目标是用最少的“切片”次数把所有塔变平。一个很自然的想法是：让每一次切片都尽可能地多切一些，直到成本快要超出限制 k 为止。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    // Faster input/output
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(NULL);

    int n;
    long long k;
    std::cin >> n >> k;

    // Use a vector as a frequency map for heights
    std::vector<int> counts(200002, 0);
    int min_h = 200001;
    int max_h = 0;

    for (int i = 0; i < n; ++i) {
        int h;
        std::cin >> h;
        counts[h]++;
        min_h = std::min(min_h, h);
        max_h = std::max(max_h, h);
    }

    // If all towers are already the same height, no slices are needed.
    if (min_h == max_h) {
        std::cout << 0 << "\n";
        return 0;
    }

    long long slices = 0;
    long long current_slice_cost = 0;
    long long towers_to_cut = 0; // Number of towers taller than the current height h

    // Iterate level by level from the top
    for (int h = max_h; h > min_h; --h) {
        // Add the towers AT the current height h to the group that needs cutting.
        towers_to_cut += counts[h];

        // If there are no towers to cut this high, just continue.
        if (towers_to_cut == 0) {
            continue;
        }

        // Check if adding the cost of one more layer exceeds the limit k
        if (current_slice_cost + towers_to_cut > k) {
            // If it does, we must perform a slice.
            slices++;
            // The new slice starts with the cost of the current layer.
            current_slice_cost = towers_to_cut;
        } else {
            // Otherwise, add the cost to the current slice.
            current_slice_cost += towers_to_cut;
        }
    }

    // If there's any remaining cost, it means one last slice was made.
    if (current_slice_cost > 0) {
        slices++;
    }

    std::cout << slices << "\n";

    return 0;
}